In machine learning, selecting the appropriate model and tuning hyperparameters are fundamental for achieving optimal results. GridSearchCV is a powerful tool that automates these processes, saving time and improving accuracy. This tutorial will guide you through the use of GridSearchCV, explaining its functionality, advantages, and practical applications. You will learn how to set up your environment, prepare data, and apply GridSearchCV both for a specific algorithm and to compare multiple models.

The purpose of this tutorial is to provide a deep understanding of GridSearchCV and its implementation in Python. By the end of this tutorial, you will be able to configure and use GridSearchCV for one or multiple algorithms, interpret the results to select the best model and its hyperparameters, and achieve machine learning model optimization efficiently and automatically.

To follow this tutorial, it is recommended to have basic knowledge of Python and fundamental machine learning concepts, including classification, cross-validation, and evaluation metrics. We will be using the scikit-learn library to implement GridSearchCV and various machine learning algorithms, pandas for data handling and processing, seaborn to load the example dataset, and numpy for numerical operations.

Whether you’re a beginner or an expert, this tutorial will provide you with the necessary skills to efficiently optimize your machine learning models.

What is GridSearchCV and how does it work?

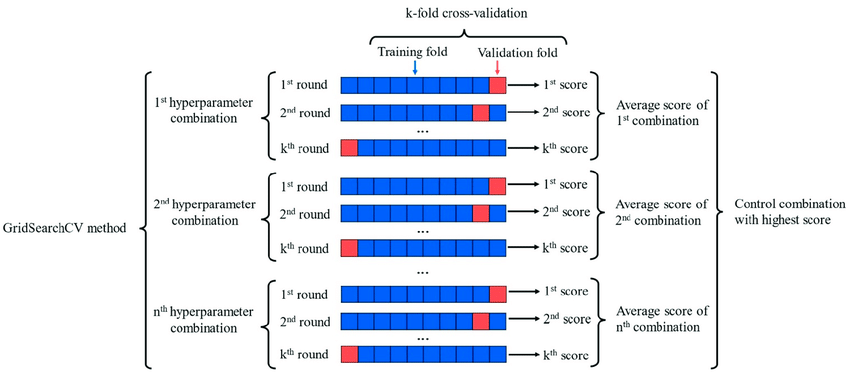
GridSearchCV is a technique used in Machine Learning to find the optimal hyperparameters of a model based on the dataset to be used. In this method, the user establishes a grid of hyperparameters which is used to evaluate multiple possible combinations and select the best one based on a performance metric specified by the user.

Source: Shear Strength Prediction of Slender Steel Fiber Reinforced Concrete Beams Using a Gradient Boosting Regression Tree Method

There are several alternative methods for hyperparameter tuning, each with its own advantages in different scenarios. For example, RandomizedSearchCV randomly selects combinations of hyperparameters, being more efficient than GridSearchCV in large search spaces. On the other hand, we have Bayesian optimization, which uses probabilistic models to predict the most promising combinations.

GridSearchCV is ideal for small to medium search spaces and when sufficient computational resources are available. It is particularly useful when deterministic and reproducible results are needed, or when seeking to thoroughly understand the impact of each hyperparameter combination. This method is suitable for smaller-scale problems with smaller datasets or less complex models. In contrast, for larger search spaces or when computation time is limited, methods like RandomizedSearchCV or Bayesian optimization may be more appropriate. The choice of method will depend on the balance between search thoroughness, available time, and computational resources. GridSearchCV offers a complete search and is ideal for thoroughly understanding the hyperparameter space, but it can become inefficient for more complex problems where more advanced methods may offer a better balance between exploration and computational efficiency.

The following comparative chart provides an overview of the three main hyperparameter tuning methods mentioned above. This table can serve as a valuable guide when selecting the most appropriate approach for your specific machine learning project. Each column represents a key feature to consider, allowing you to evaluate which method best aligns with the needs and constraints of your particular problem.

What is Cross-validation?

This is a statistical method used to estimate the ability of machine learning models. Its process includes splitting the dataset, training the model on a portion of the data, and validating it on the remaining portion. This cycle is repeated multiple times to ensure the model’s performance is consistent and that each data point has a chance to be validated against the model.

As we mentioned before, when using GridSearchCV all combinations of the values in the hyperparameter grid are tested and the model is evaluated in each combination, due to the use of the cross-validation method.

Advantages of using GridSearchCV

Exhaustively searches through each parameter combination
Once configured, it runs without manual intervention to tune the model
Helps find the best hyperparameters of a model, potentially improving its performance
Its configurability allows control over desired hyperparameter combinations

Common Use Cases

Hyperparameter tuning for Machine Learning algorithms
Optimization of Deep Learning model architectures
Selection of the best algorithm for a specific dataset

Some Limitations

Can be time and resource-intensive with large parameter grids
Care must be taken not to overfit the validation set
Performance may degrade with too many parameters, in other words, the “curse of dimensionality”

Common Errors when using GridSearchCV and their Solutions

1. Defining too broad a search space, which can result in excessively long execution times

Solution: Start with a narrower range of hyperparameters and gradually refine

2. Overfitting, which can occur when using an inappropriate evaluation metric or when cross-validation is not properly implemented

Solution: Carefully select the evaluation metric depending on the problem and ensure proper cross-validation configuration

3. Memory errors, especially with large datasets or complex models

Solution: Reduce dataset size, use batch processing, or consider alternatives like RandomizedSearchCV

4. Misinterpretation of results, as the best model according to GridSearchCV may not necessarily be the best for unseen data

Solution: Perform additional validation with a separate test dataset

5. Lack of reproducibility can be an issue if a random seed is not set

Solution: Fix the random seed for both the model and data splitting to ensure consistent results

How to use GridSearchCV?

In this tutorial, I’ll be using Jupyter Notebook integrated into Visual Studio Code, running a Python 3.12 kernel. To make it easier to follow along and allow for a more detailed exploration, the source code is already available in our GitHub repository. Please check it out if you want to follow the tutorial step-by-step or dig deeper into specific aspects of the code.

1. Environment setup: Install and import the necessary libraries.

First, we will install the Scikit-Learn, pandas, seaborn, matplotlib and numpy libraries in our virtual environment with the following command:

pip install scikit-learn pandas seaborn matplotlib numpy

GridSearchCV comes from the Scikit-Learn python library, while we will be using the Pandas library for dataset management and Seaborn to import the dataset.

Then we import the installed libraries and the functions to use:

from sklearn.model_selection import GridSearchCV, train_test_split
import seaborn as sns
import numpy as np
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
from matplotlib import pyplot as plt

2. Prepare the dataset

For this example, we will be using the “healthexp” dataset from the Seaborn library and our target variable will be the “Country” column. This dataset was selected due to its manageable size and its combination of numerical and categorical features, making it ideal for demonstrating the use of GridSearchCV without requiring extensive computational resources. Its content, which relates health expenditure to life expectancy in different countries, provides an interesting and accessible context for a wide audience.

In this case, I decided to use the “dropna” function to filter and remove null values from the dataframe.

target_variable = "Country"
df = sns.load_dataset("healthexp")
df.dropna(inplace=True)
X = df.drop(target_variable, axis=1)
y = df[target_variable]

And then we split the data into training and test sets.

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

3. Parameter grid

Before diving into the code, let’s first define what hyperparameters are and what this grid received by the GridSearchCV function consists of.

Hyperparameters are external configuration parameters to a machine learning model that are not learned directly from the data during training; they control the learning process and the structure of the model. Unlike the regular parameters of the model, hyperparameters are set before training and affect how the model learns from the data.

The “grid” in GridSearchCV is essentially a dictionary or list of dictionaries that specifies the values to be tested for each hyperparameter. In this tutorial, two distinct approaches to using grids will be shown: The first will focus on hyperparameter tuning for a specific algorithm, while the second will focus on selecting the most efficient algorithm within a set, along with optimizing their respective hyperparameters. These two strategies will allow us to explore both individual model optimization and comparison and selection between multiple algorithms.

# EXAMPLE
param_grid = {
    'C': [0.1, 1, 10, 100],
    'kernel': ['rbf', 'linear'],
    'gamma': ['scale', 'auto', 0.1, 1]
}

In this example of a grid for an SVM classifier, GridSearchCV will test all the combinations of these values, resulting in 4 * 2 * 4 = 32 different hyperparameter combinations.

4. Implementation of GridSearchCV

Before starting, I recommend reviewing the original documentation of GridSearchCV to better understand the parameters passed to the function. Here is a brief summary of each one:

estimator: Pass the model instance for which you want to check the hyperparameters.
params_grid: The dictionary object that holds the hyperparameters you want to try (Our parameter grid)
scoring: Evaluation metric that you want to use. You can simply pass a valid string/object of evaluation metric.
cv: Number of cross-validation you have to try for each selected set of hyperparameters.
verbose: You can set it to 1 to get the detailed print out while you fit the data to GridSearchCV.
n_jobs: number of processes you wish to run in parallel for this task. If it is -1, it will use all available processors.

(Great Learning Editorial Team, 2024)

Now, let’s continue with the implementation!

For a specific algorithm

# Define the base model, in this case we will use Random Forest Classifier
rf = RandomForestClassifier(random_state=23)

# Define the parameter grid
param_grid = {
    'n_estimators': [50, 100, 200],
    'max_depth': [None, 5, 10],
    'min_samples_split': [2, 5, 10],
    'min_samples_leaf': [1, 2, 4]
}

# Configure GridSearchCV
grid_search = GridSearchCV(estimator=rf, param_grid=param_grid, cv=5, scoring='accuracy', n_jobs=-1, verbose=2)

# Fit GridSearchCV
grid_search.fit(X_train, y_train)

# Evaluate the model with the best parameters on the test set
best_model = grid_search.best_estimator_
test_accuracy = best_model.score(X_test, y_test)

Don’t worry if the code takes a while to run, as this depends on the size of the dataset and our grid. Try modifying the number of parameters used in the example to see the difference 😉.

Now, let’s continue with the visualization of the results:

# Display the best parameters and the best score
print(f'Best parameters: {grid_search.best_params_}')
print(f'CV Score: {round(grid_search.best_score_,2)}')
print(f'Test Score: {round(test_accuracy,2)}')

Output on the console with the best parameters and scores

# Predict the labels of the test set
y_pred = best_model.predict(X_test)

# Compute the confusion matrix
cm = confusion_matrix(y_test, y_pred)

# Show the confusion matrix
disp = ConfusionMatrixDisplay(
    confusion_matrix=cm, display_labels=best_model.classes_)
disp.plot(cmap='Blues')

Confusion matrix for Random Forest model

As we can see from the output, the best parameters to use for this dataset with the Random Forest model are: ‘max_depth’=’None’, ‘min_samples_leaf’=1, ‘min_samples_split’=2, and ‘n_estimators’=200. This time, we achieved a test set score of 0.67 and a cross-validation score of 0.72. Can we achieve a better score using other models? Let’s find out!

To find the most optimal algorithm within a set

Implementing GridSearchCV for multiple algorithms can be a bit complex, so in this case, we will go step by step.

1. Definition of models and parameters:

# Define the models and their respective parameters for GridSearchCV
models = [
    ("Decision Tree", DecisionTreeClassifier(random_state=23), 
        {'max_depth': range(1, 15)}),
    ("Random Forest", RandomForestClassifier(random_state=23), 
        {'n_estimators': [50, 100, 200, 300], 'max_depth': [None, 2, 3, 5, 7, 10]}),
    ("Gradient Boosting", GradientBoostingClassifier(random_state=23), 
        {'n_estimators': [50, 100, 200], 'learning_rate': [0.01, 0.1, 1]}),
    ("K Nearest Neighbors", KNeighborsClassifier(), 
        {'n_neighbors': [3, 5, 7, 10]})

First, we’ll define a list of tuples, where each one will have the model name, the model instance, and a dictionary with the parameters of that model to be used in GridSearchCV. In this example, we will work with 4 models: Decision Tree, Random Forest, Gradient Boosting, and K Nearest Neighbors, all classifiers. For the hyperparameters of the Random Forest in this case, we will only focus on n_estimators and max_depth to see if we obtain any change compared to the previous example.

2. Training, evaluation, and selection of the best model:

# Initialize dictionaries and variables to store results
results = {}
best_models = []
best_stability = np.inf
best_test_score = -np.inf  # For classification, we want to maximize the score

# Iterate over each model and its parameters
for name, model, params in models:
    # Configure and fit GridSearchCV
    grid = GridSearchCV(estimator=model, param_grid=params,
                        cv=5, scoring='accuracy', verbose=1)
    grid.fit(X_train, y_train)
    test_score = grid.score(X_test, y_test)

    # Calculate model stability (difference between best cross-validation score and test score)
    stability = abs(grid.best_score_ - test_score)

    # Store the current model's results
    results[name] = {
        "best_cv_score": round(abs(grid.best_score_), 2),
        "test_score": round(abs(test_score), 2),
        "stability": round(stability, 2),
        "best_params": grid.best_params_,
    }

    # Update the best model if necessary
    if test_score > best_test_score or (test_score == best_test_score and stability < best_stability):
        best_test_score = test_score
        best_cv_score = grid.best_score_
        best_stability = stability  # Update the best stability
        # Start a new list of best models
        best_models = [
            (name, grid.best_params_, round(best_cv_score, 2), round(best_test_score, 2))
        ]
    elif test_score == best_cv_score:
        best_models.append((name, grid.best_params_))  # Add the current model to the best models list

# Confusion matrix for each of the models
y_pred_best = grid.predict(X_test)
cm_best = confusion_matrix(y_test, y_pred_best)
disp_best = ConfusionMatrixDisplay(confusion_matrix=cm_best, display_labels=grid.best_estimator_.classes_)
disp_best.plot(cmap='Blues')
plt.title(f'Confusion Matrix for {name}')
plt.show()

Confusion Matrix for Decision Tree model

Confusion Matrix for Gradient Boosting model

Confusion Matrix for K Nearest Neighbors model

This part of the tutorial may take significantly longer than the previous one, as we are performing Grid Search on four different models.

Notes:

The score on the test set and stability are calculated, with stability being the difference between the best cross-validation score and the test score.
The best model is updated based on the test score and stability.
In case of a tie in the score, multiple models are considered as “best”.

3. Final results:

In the code, the results are saved in the following variables:

best_stability: Contains the stability of the best model(s).
best_models: A dictionary containing the best model(s) for the dataset along with their optimal parameters and scores.
results: A dictionary with all the results of each evaluated model.

In our Jupyter Notebook (link to the repository), these can be visualized as follows:

Output on the console with the best model, its scores and the best parameters

The results confirm that the Random Forest model remains the most effective option among the algorithms evaluated for this dataset. This model maintained its robust and consistent performance, achieving a cross-validation score of 0.72 and a test set score of 0.67.

Interestingly, these results are identical to those obtained in our previous example, suggesting that we had already reached an optimal level of performance with our initial configuration. The decision to focus specifically on the hyperparameters ‘max_depth’ and ‘n_estimators’ during this new tuning process did not lead to additional improvements, indicating that the original calibration was already quite accurate.

This experience highlights the importance of recognizing when a satisfactory level of optimization has been reached. It demonstrates that further adjustments are not always necessary if good performance has already been achieved. In future analyses, it will be valuable to consider this finding and carefully evaluate whether further iterations of optimization are needed or if resources might be better utilized in other aspects of the model or in exploring different approaches.

Table with the performance of each model

In this table, we can visualize the performance of each tested model and their respective parameters. We can conclude that the Random Forest model shows the best performance among all the evaluated models, with the highest scores in both cross-validation (CV) and the test set. Although it doesn’t have the perfect stability of Gradient Boosting, its stability of 0.05 is very good, indicating that the model generalizes well and does not suffer from overfitting.

Optimizing GridSearchCV Performance

To reduce the computational load when using GridSearchCV, there are several effective strategies, such as using a smaller subset of the dataset for the initial hyperparameter tuning. This allows for rapid exploration of the hyperparameter space, identifying promising areas that can later be refined with the full dataset. Another common technique is parallelizing the search using the n_jobs parameter in GridSearchCV. By setting n_jobs=-1, all available processor cores are utilized, significantly speeding up the search process. Additionally, a two-stage search strategy can be implemented: first, a broad but shallow search to identify promising regions, followed by a more detailed search in these areas.

When it comes to hyperparameter selection, it is crucial to focus on those that have the most significant impact on the model’s performance. For example, in tree-based models like Random Forest or Gradient Boosting, parameters such as the maximum tree depth, the number of estimators, and the learning rate are often critical. It is advisable to start with a wide range for these key parameters and then refine them based on initial results. It is also useful to consult literature and previous studies on similar problems to gain insights into which hyperparameters tend to be most impactful for each type of model and specific problem.

Key points to remember:

GridSearchCV automates the search for the best combination of hyperparameters, significantly improving model performance.
The choice between GridSearchCV and other methods like RandomizedSearchCV mainly depends on the search space size and available computational resources.
It is crucial to carefully select the range of hyperparameters to explore, focusing on those with the most significant impact on model performance.
Techniques like parallelization (n_jobs) and the use of data subsets can significantly reduce computation time.
GridSearchCV is a versatile tool applicable to a wide range of machine learning algorithms, from simple regressions to more complex models.

Throughout this tutorial, we delved into the importance of model selection and hyperparameter tuning in the realm of machine learning, and we learned that GridSearchCV is a fundamental tool that automates these processes, allowing users to evaluate multiple hyperparameter combinations systematically and efficiently. We covered the basics of GridSearchCV, its functionality, and its advantages, as well as alternative techniques that may be more suitable in certain contexts.

If you’ve made it this far, it means you are now equipped to implement GridSearchCV in your own machine learning projects, interpret the obtained results, and apply a systematic approach to model optimization. With this foundation, you will be better prepared to tackle machine learning challenges and continue developing your skills in this ever-evolving field.

Conclusion

The importance of hyperparameter tuning and algorithm selection in machine learning cannot be underestimated. As we saw in this tutorial, implementing GridSearchCV allows us to automate these crucial processes, leading to more robust and accurate models. This can be practically applied in various fields. For example, in credit card fraud detection, optimizing classification models like Random Forest or SVM by tuning key parameters enhances the identification of fraudulent transactions. In customer segmentation for marketing, GridSearchCV is applied to clustering algorithms like K-Means, refining parameters to achieve more meaningful segmentations. In housing price prediction, it optimizes regression models like Gradient Boosting or Neural Networks, minimizing prediction error. In these and many other cases, GridSearchCV helps find the optimal combination of hyperparameters, improving model performance and increasing prediction accuracy for specific real-world problems. However, it’s also crucial to be aware of common errors, such as overfitting the validation set, defining too broad search spaces, or misinterpreting results. These errors can be avoided through nested cross-validation, a two-stage search strategy, or a deep understanding of the evaluation metrics used. By keeping these potential errors in mind, GridSearchCV’s effectiveness in real-world applications can be maximized.

GridSearchCV facilitates a systematic and objective way to compare different algorithms, helping us choose the most suitable one for our specific dataset. Although the process can be computationally intensive, it automates a task that would be extremely tedious and error-prone if done manually, saving valuable time and resources.

Looking ahead, several steps and alternatives can be considered to expand and improve our approach. These include exploring wider hyperparameter spaces, adding more values or even additional hyperparameters for each algorithm. While GridSearchCV is effective, alternatives like RandomizedSearchCV or Bayesian optimization methods can be more efficient for larger hyperparameter spaces and are worth investigating.

Exploring other metrics relevant to a specific problem, such as F1-score, AUC-ROC, or domain-specific metrics, can also provide a more complete picture of model performance. Finally, a crucial step would be exploring how to integrate this model selection and tuning process into a production machine learning workflow, taking our findings from theoretical to practical application.

By adopting a systematic approach and exploring various tools and techniques, you’ll be better prepared to face machine learning challenges and continuously improve your skills 😁.

Automating Model Selection and Hyperparameter Tuning with GridSearchCV